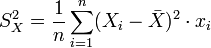medidas de dispersion

Publicado en 19 junio 2010 por lesy

Las medidas de dispersión, también llamadas medidas de variabilidad, muestran la variabilidad de una distribución, indicando por medio de un número, si las diferentes puntuaciones de una variable están muy alejadas de la media. Cuanto mayor sea ese valor, mayor será la variabilidad, cuanto menor sea, más homogénea será a la media. Así se sabe si todos los casos son parecidos o varían mucho entre ellos.

Para calcular la variabilidad que una distribución tiene respecto de su media, se calcula la media de las desviaciones de las puntuaciones respecto a la media aritmética. Pero la suma de las desviaciones es siempre cero, así que se adoptan dos clases de estrategias para salvar este problema. Una es tomando las desviaciones en valor absoluto (Desviación media) y otra es tomando las desviaciones al cuadrado (Varianza).

Rango estadístico

El rango o recorrido estadístico es la diferencia entre el valor mínimo y el valor máximo en un grupo de números aleatorios. Se le suele simbolizar con R.

Requisitos del rango

Ordenamos los números según su tamaño.
Restamos el valor mínimo del valor máximo.

Ejemplo

Para una muestra (0, 45, 50, 55, 100), el dato menor es 0 y el dato mayor es 100 (Valor unitario inmediatamente posterior al dato mayor menos el dato menor). Sus valores se encuentran en un rango de:

Rango = (100-0) =100

Medio rango

El medio rango de un conjunto de valores numéricos es la media del menor y mayor valor, o la mitad del camino entre el dato de menor valor y el dato de mayor valor. En consecuencia el medio rango es:

$medioRango = \frac{\ (Min + Max)}{2}$

Ejemplo

Para una muestra de valores (3, 3, 5, 6, 8), el dato de menor valor Min= 3 y el dato de mayor valor Max= 8. El medio rango resolviendolo mediante la correspondiente fórmula sería:

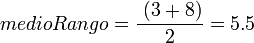
$medioRango = \frac{\ (3 + 8)}{2} = 5.5$

Representación del medio rango:

Varianza

La varianza, también denominada variancia (Aunque esta denominación es menos elegida) es una medida estadística que mide la dispersión de los valores respecto a un valor central (media), es decir, la media de las diferencias cuadráticas de las puntuaciones respecto a su media aritmética. Suele ser representada con la letra griega σ o una V en mayúscula.

$S_X^2 = \frac{\sum_{i=1}^n (X_i - \bar{X})^2}{n}$

$S_X^2 = \frac{1}{n}\sum_{i=1}^n (X_i - \bar{X})^2 \cdot x_i$

Propiedades

La varianza es siempre positiva o 0: $S_{X}^2 \geq 0$
Si a los datos de la distribución les sumamos una cantidad constante la varianza no se modifica.

$Y i = X i + k$ c $S_Y^2 = \frac{\sum (Y_i - \bar{Y})^2}{n} = \frac{\sum [(X_i + k) - (\bar{X} + k)]^2}{n} = \frac{\sum (X_i + k - \bar{X} - k)^2}{n} = \frac{\sum (X_i - \bar{X})^2}{n} = S_X^2$

Si a los datos de la distribución les multiplicamos una constante, la varianza queda multiplicada por el cuadrado de esa constante.

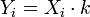
$Y_i = X_i \cdot k$

$S_Y^2 = \frac{\sum (Y_i - \bar{Y})^2}{n} = \frac{\sum (X_i \cdot k - \bar{X} \cdot k)^2}{n} = \frac{\sum [k \cdot (X_i - \bar{X})]^2}{n} = \frac{\sum [k^2 \cdot (X_i - \bar{X})^2]}{n} = k^2 \cdot \frac{\sum (X_i - \bar{X})^2}{n} = k^2 \cdot S_X^2$

Propiedad distributiva: $V (X + Y) = V (X) + V (Y)$

Desviación típica

La variancia a veces no se interpreta claramente, ya que se mide en unidades cuadráticas. Para evitar ese problema se define otra medida de dispersión, que es la desviación típica, o desviación estándar, que se halla como la raíz cuadrada positiva de la varianza. La desviación típica informa sobre la dispersión de los datos respecto al valor de la media; cuanto mayor sea su valor, más dispersos estarán los datos. Esta medida viene representada en la mayoría de los casos por S, dado que es su inicial de su nominación en inglés.

Desviación típica muestral

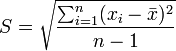
$S = \sqrt{\frac{\sum_{i=1}^n (x_i - \bar{x})^2}{n-1}}$

Desviación típica poblacional

$\sigma = \sqrt{\frac{\sum_{i=1}^n (X_i - \mu)^2}{N}}$

Ejemplo

Con Scilab este cálculo se hace de la siguiente manera:

 -->x= [17 14 2 5 8 7 6 8 5 4 3 15 9] x = 17. 14. 2. 5. 8. 7. 6. 8. 5. 4. 3. 15. 9. -->stdev(x) ans = 4.716311 -->

Primero hemos declarado un vector con nombre X, donde introduzco los números de la serie. Luego con el comando stdev se hallará la desviación típica.

Covarianza

La covarianza entre dos variables es un estadístico resumen indicador de si las puntuaciones están relacionadas entre sí. La formulación clásica, se simboliza por la letra griega sigma (σ) cuando ha sido calculada en la población. Si se obtiene sobre una muestra, se designa por la letra "s_{xy}".

La formula suele aparecer expresada como:

$\hat{S}_{xy} = \frac{\sum_{i=1}^n x_i y_i}{n-1} = \frac{\sum_{i=1}^n (X_i - \bar{X})(Y_i - \bar{Y})}{n-1}$

Este tipo de estadístico puede utilizarse para medir el grado de relación de dos variables si ambas utilizan una escala de medida a nivel de intervalo/razón (variables cuantitativas).

La expresión se resuelve promediando el producto de las puntuaciones diferenciales por su tamaño muestral (n pares de puntuaciones, n-1 en su forma insesgada). Este estadístico, refleja la relación lineal que existe entre dos variables. El resultado numérico fluctua entre los rangos de +infinito a -infinito. Al no tener unos límites establecidos no puede determinarse el grado de relación lineal que existe entre las dos variables, solo es posible ver la tendencia.

$-\infty \leq S_{xy} \leq +\infty$
$S_{xy} = \begin{cases} > 0, & \mbox{Correlaci}\acute{o}\mbox{n directa. Recta de regresi}\acute{o}\mbox{n creciente.} \ = 0, & \mbox{No hay correlaci}\acute{o}\mbox{n.} \ < 0. & \mbox{Correlaci}\acute{o}\mbox{n inversa. Recta de regresi}\acute{o}\mbox{n decreciente.} \end{cases}$

Ejemplo

Tenemos una tabla con dos datos (x y h), elaboramos su tabla de frecuencias (fre)

 -->x=[10 20 30 40] Vector de datos X x = 10. 20. 30. 40. -->y=[10 20 30 40] Vector de datos H y = 10. 20. 30. 40. -->fre=[.20 .04 .01 0; Matriz de frecuencias --> .10 .36 .09 0; --> 0 .05 .10 0; --> 0 0 0 .05] fre = 0.2 0.04 0.01 0. 0.1 0.36 0.09 0. 0. 0.05 0.1 0. 0. 0. 0. 0.05 -->s=covar(x,y,fre) Aplicación del Comando covar s =